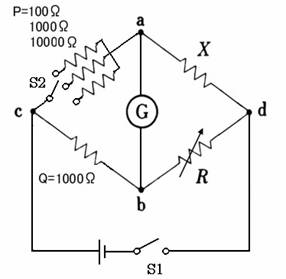
�P�D�ړI
�@�@�@�g�̎���ɂ���d�����i��������u�Ȃǂ́A�P�O�O�u�̌𗬓d���ł��d�͂č쓮���Ă���B�������Ȃ���A�����̑��u�͒����d���ō쓮����̂ŁA�𗬂��ɕϊ����Ă��炵�Ȃ���Ȃ�Ȃ��B���̂悤�ȕϊ���H�͉�X���g�����i�ɑg�ݍ��܂�Ă���B
�@�@�@��L�̂��Ƃ܂�����ŁA�ϊ���H��p���Č𗬂��璼���ɕϊ����I�V���X�R�[�v�̔g�`�����Ċm�F����B����ɕϊ���H�Ɏg���Ă����v�d�C��H���i�ƃz�C�[�X�g���u���b�W��H�̖�������𗝉�����B
|
|
�Q�D�z�C�[�X�g���u���b�W��H
�@(�T)��������
�@�@(1)�d���X�C�b�`�r�P���I�t�ɂ���B
�@�@(2)��R�o�̐�ւ��X�C�b�`�𒆉���
1000[��]�ɂ���B
�@�@(3)�e�X�^�[�̒[�q�����̂f�P�Ƃf�Q
�@�@�ɍ������ށB(�}�P�ł͂f�P�Ƃf�Q�́A
���Ƃ��̈ʒu�ł���)
(4)���m��R�w���P�I��ŁA��Տ�̂s�P
�Ƃs�Q�ɍ������ށB(�}�P�ł͂s�P�Ƃs�Q
�́A���Ƃ��̈ʒu�ł���)
�@�@(5)�e�X�^�[�̃��[�^���[�X�C�b�`�����`��
�Z�b�g����B
�@�@(6)�d���X�C�b�`���I���ɂ���B
�@�@(7)�e�X�^�[�̓d���l���[���ɂȂ�悤�ɉϒ�R�q�߂���B
�@�@(8)�����q�߂��Ă��d���l���[���ɂȂ�Ȃ���A�f�[�^�V�[�g�Ɂg����s�\�h�Ə����Ăr�Q���A100[��]�y��10000(10k) [��]�ɐ�ւ��āA�Ă�(7)�̑�����J��Ԃ��B
�@�@(9)���`�����W�œd�����[���ɂȂ�����A�e�X�^�[�̃��[�^���[�X�C�b�`���ʂ`�̃����W�ɐ�ւ��āA�q�߂��ēd���l���[���ɂ���B
�@�@(10)�d���l���[���ɂȂ����Ƃ��̂q�̒�R�l��ǂݎ��B
�@�@(11)�R��ނ̈قȂ��R�l�̒�R�q�ɂ��āA(7)�`(10)�̑�����J��Ԃ��A�ʂ`�����W�œd���l���[���ɂȂ����Ƃ��̂q�̒l��ǂݎ��B
�@�@(12)�ȏ�̑�����J��Ԃ��āA���m��R�w�P�{�ɂ��āA�قȂ�R�̒�R�o���g���đ�������鑪�肪�I�������A�r�P���I�t�ɂ��Ă����R�̎��O�����s���B
�@�@(13) (4)�`(12)�̑�����J��Ԃ��āA�T�{�̖��m��R�w���ׂĂ𑪒肵�A�\�ɂ���
�@�@(14)�Ō�ɁA�e�X�^�[�̒�R�l���胂�[�h���g���A�T�{�̖��m��R�w�̒�R�l�𑪒肵�āA(13)�ō쐬�����\�ɂ܂Ƃ߂�B
�@�i�U�j����
�@�@�@�@�@�����ő��肵���l���ȉ��̕\1�ɂ܂Ƃ߂��B���肵���o�Ƃp���疢�m��R�w�̒�R�l���Z�o�������@�͈ȉ��̎��ł���B���̎��͗e�Ղɓ��o�ł���B
![]() �@�@�@�@�i�P�j
�@�@�@�@�i�P�j
�@�@�@�@�@�������A����̎����ł͂p�̒�R���̒�R�l1000[��]�ł���B
�\�P�@���m��R�w�̑���
|
�w (No.) |
�o [��] |
�q [��] |
�w(�����l) [��] |
�w(�����l) [��] |
|
|
C |
100 |
�@ |
272
|
2.72�~10 |
�@ |
|
1000 |
�@ |
27
|
2.7 �~10 |
27.3 |
|
|
10000 |
�@ |
3
|
3 �~10
|
�@ |
|
|
F |
100 |
�@ |
����s�\ |
����s�\ |
�@ |
|
1000 |
�@ |
266 |
2.66�~102 |
269.1 |
|
|
10000 |
�@ |
28 |
2.8�@�~102 |
�@ |
|
|
G |
100 |
�@ |
����s�\ |
����s�\ |
�@ |
|
1000 |
�@ |
����s�\ |
����s�\ |
5.59�~103 |
|
|
10000 |
�@ |
555 |
5.55�~103�@�@ |
�@ |
|
|
H |
100 |
�@ |
����s�\ |
����s�\ |
�@ |
|
1000 |
�@ |
����s�\ |
����s�\ |
2.981�~103 |
|
|
10000 |
�@ |
294
|
2.94�~103 |
�@ |
|
|
I |
100 |
�@ |
����s�\ |
����s�\ |
�@ |
|
1000 |
�@ |
193
|
1.93�~102 |
198.0 |
|
|
10000 |
�@ |
19
|
1.9 �~102 |
�@ |
|
�i�V�j�l�@
�@�@�@�@�R��̈قȂ��R�l�̂o���g���āA���m��R�w�̒�R�l���R�푪��ł����f�[�^�͂b�����Ȃ��B�������A�Q��܂ł̒�R�l���Z�o�ł����f�[�^�͂Q����̂ł����̒l����l�@���s���B
�@�@�@�@�o�̒�R�l���傫���Ȃ�ƁA�ς�����q�̒�R�l���������Ȃ�A����ł����R�l�̌������������Ȃ��Ă���B����͉ϒ�R�q�̖ڐ���̍ŏ��̈ʂ��P�ł��邽�߂ł���B�o�̒�R�l���������ƁA����ł���q�̒l���傫���Ȃ茅���𑽂������̂ŁA�L�������������đ��萸�x�������Ȃ�ƍl������B�܂� (�P)�����A�w�Ƃp�����ƍl����ƁA�o�Ƃq�͔����̊W�ɂ��邱�Ƃ��킩��B�ϒ�R�q�̑���ł��錅�͈͓̔��ł���A�o����������q�͑傫���Ȃ�̂ŁA����ł��錅���������Ȃ葪�萸�x�͍����Ȃ�B
�@�@�@�@�����ŁA�o�C�p�C�q�̒�R�l���ǂ̂悤�Ȓl�ɂ���A�w�̒l�̎Z�o���x���オ�邩�l����B�܂��A��R��̐��x�덷���P���Ƃ���B
�@�@�@�@�ϒ�R�q�̉ω\�Ȕ͈͂͂P�`�X�X�X[��]�ł���B���̎�����A�w���Z�o����̂ɐ��x����������ɂ́A�q�̒l���R���ɂ���̂��ł��ǂ��ƍl������B���̂Ƃ��ɑ��肷�関�m��R�w�̒�R�̑傫���ɂ���邪�A�d���d�����ɂ����ꍇ�A�p�̒l��������x������������������̊��x�͏オ��ƍl������B�p�̒�R�����������߂���ƁA���M��[�h����R�̌덷�ɉe������Ă��܂��̂ŁA�K�������p�̒�R�l���������قǂ����Ƃ͂����Ȃ��B
�R�D�T�[�~�X�^
�@�i�T�j��������
�@�@�@(1)�T�[�~�X�^����o�Ă���Q�{�̒[�q���A�u���b�W��H���̂s�P�Ƃs�Q�ɍ������ށB
�@�@�@(2)�T�[�~�X�^���P���w�ɓ���A�P�����̉��x���R�O���ɐݒ肷��B
�@�@�@(3)�P�����̉��x�����ɂȂ�����A�u���b�W��H���g���ăT�[�~�X�^�̒�R�l�𑪒肷��B��ւ���R�o�͑���ł��邷�ׂẴ����W�ɂ��čs���B
�@�@�@(4)�R�O�`�V�O���̊Ԃ��P�O���Ԋu��(2)��(3)�̑�����J��Ԃ��āA�e���x�ł̒�R�l�𑪒肷��B
(5)�V�O���̑�����I��������A�T�[�~�X�^��X���ŗ�p���ĂO���ɂ������R�l�𑪒肷��B
(6)�r�P���I�t�ɂ��ăT�[�~�X�^���u���b�W��H����O���A�ς��ɗp�ӂ��Ă����R������t����B
(7)�V�O���ƂO���ɂ������R�l���u���b�W��H�Ɨp���đ��肷��B
(8)���ׂĂ̑��肪�I��������A�r�P���I�t�ɂ��Ē�R����O���A�P�����̓d�����I�t�ɂ���B
�i�U�j����
�@�@�@�@�@�����ő��肵���l���ȉ��̕\�Q�ƕ\�R�ɂ܂Ƃ߂��B
�\�Q�@�T�[�~�X�^
|
���x
[��] |
�o[��] |
�q [��] |
��R�l [��] |
|
|
0 (0) |
100 |
�@ |
����s�\ |
����s�\ |
|
1000 |
�@ |
506
|
5.06�~102�@�@ |
|
|
10000 |
�@ |
52
|
5.2�~102�@�@ |
|
|
30 (29.8) |
100 |
�@ |
����s�\ |
����s�\ |
|
1000 |
�@ |
182
|
1.82�~102�@�@ |
|
|
10000 |
�@ |
19
|
1.9 �~102�@ |
|
|
40 (40.6) |
100 |
�@ |
975
|
9.75�~10�@�@ |
|
1000 |
�@ |
130
|
1.30�~102�@�@ |
|
|
10000 |
�@ |
13
|
1.3�@�~102�@�@ |
|
|
50 (50.6) |
100 |
�@ |
729
|
7.29�~10�@�@ |
|
1000 |
�@ |
94
|
9.4�@�~10�@�@ |
|
|
10000 |
�@ |
10
|
1.0�@�~102�@�@ |
|
|
60 (59.8) |
100 |
�@ |
566
|
5.66�~10�@�@ |
|
1000 |
�@ |
72
|
7.2�@�~10�@�@ |
|
|
10000 |
�@ |
8
|
8�@�@�~10�@�@ |
|
|
70 (69.4) |
100 |
�@ |
444
|
4.44�~10�@�@ |
|
1000 |
�@ |
55 |
5.5�@�~10�@�@ |
|
|
10000 |
�@ |
6 |
6�@�~10�@�@ |
|
�\�R�@��R��
|
���x
[��] |
�o[��] |
�q [��] |
��R�l [��] |
|
|
0 (0) |
100 |
�@ |
994 |
9.94�~10 |
|
1000 |
�@ |
100 |
1.00�~102 |
|
|
10000 |
�@ |
11 |
1.1�@�~102
|
|
|
70 (69.4) |
100 |
�@ |
1000 |
1.000�~102 |
|
1000 |
�@ |
100 |
1.00�@�~102
|
|
|
10000 |
�@ |
10 |
1.0�@�@�~102
|
|
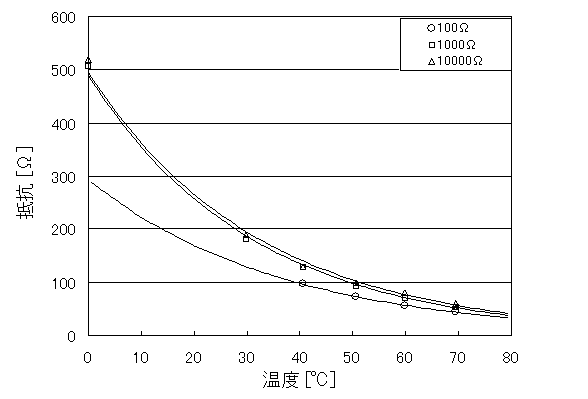 �}�P�@�T�[�~�X�^�Ɖ��x�̊W
�}�P�@�T�[�~�X�^�Ɖ��x�̊W
�@�@�@�T�[�~�X�^�Ɉȉ��̊W������̂ŁA�ߎ��Ȑ��͎w���ߎ��ŎZ�o�����B���̂Ƃ��̕��ϓ��덷��\�S�ɂ܂Ƃ߂��B
R�@=�@Ro�Eexp{B�i�P/���|�P/To�j}�@�@�@�@�@�@�@�i�Q�j
�@�@�@�@�@�@�@R�F���xT�iK�j�ɂ������R�l
�@�@�@�@�@�@�@Ro�F���xTo�iK�j�ɂ������R�l
�@�@�@�@�@�@�@B�F�萔�ł��̒P�ʂ́iK�j
�\�S�@���ϓ��덷
|
�o [��] |
100 |
1000 |
10000 |
|
���ϓ��덷 |
0.999 |
0.9984 |
0.9955 |
�@�i�V�j�l�@
�@�@�@�@�@�T�[�~�X�^�ƒ�R��Ƃ̈Ⴂ��\�Q�ƕ\�R���ׂčl�@����B
�@�@�@�@�@�T�[�~�X�^�͒�R�o�̒l�ɊW�Ȃ��A���x���㏸����ɂ�Ē�R�l�������@����X��������B����͏�L��(�Q)��������킩��B�������A��R��͉��x���㏸����ƒ�R�l����������悤�ł���B����͑��萸�x���ł������A�o���P�O�O[��]�̎��ł����ϑ����邱�Ƃ��o���Ȃ������B�Ȃ��o���P�O�O���̎��A���x�������ƌ����邩�̓z�C�[�X�g���u���b�W�̍l�@�ŋL�q�����ʂ�ł���B����ɁA�}�P�ł̕��ϓ��덷���P�O�O���̂Ƃ����ł�1.000�ɋ߂��̂Ő��x���ł������ƍl������B���x�㏸�ɔ�����R�l���オ��Ƃ����W�͒�R�킪�I�[����R�ł��邽�߂ł���B��R���̊W�������Ɏ����B
���O(�P�{����)�@�@�@�@�@�@�@�@�@�i�R�j
�����ł́A�ς͂����̒�R��[���E��]�A���O�͂O���̒�R��[���E��]�A���͉��x�㏸�P[�j]������̒�R���̑����̊���[�P�^��]�ł���B
�܂��A�T�[�~�X�^�̓_�C�I�[�h�̈��Ȃ̂ŁA��I�[����R�ł���B
�S�D�d����H
�@�i�T�j��������
(1)
�d���X�C�b�`�r�P���I�t�ɂȂ��Ă��邱�Ƃ��m�F����B
(2)
�I�V���X�R�[�v�̃W���b�N�����̃^�[�~�i���s�P�Ƃs�Q�ɍ������ށB
(3)
�d����H�̃R���Z���g���������̃e�[�u���^�b�v�ɍ������ށB
(4)
�I�V���X�R�[�v��V.ATT��GND�ASWEEP
RANGE(Hz)��10-100�ɂȂ��Ă��鎖���m�F����B
(5)
�I�V���X�R�[�v�̓d�����I���ɂ���B
(6)
![]() POSITOON�܂݂��������āA�P���𐂒����̒����ɍ��킹��B
POSITOON�܂݂��������āA�P���𐂒����̒����ɍ��킹��B
(7)
V.ATT��GND����1/100�ɓ������B
(8)
��H�̓d���X�C�b�`�r�P���I���ɂ���B�g�`���ώ@���₷�����邽�߂ɁA![]() POSITION�܂݂��������āA�g�̒��_���������ɏd�Ȃ�悤�ɂ���B
POSITION�܂݂��������āA�g�̒��_���������ɏd�Ȃ�悤�ɂ���B
(9)
���̎��̔g�`���O���t�p���ɏ������B
(10) �d���X�C�b�`�r�P���I�t�ɂ���B
(11) �s�P�Ƃs�Q�ɍ������I�V���X�R�[�v�̃W���b�N���������O���A�s�R�Ƃs�S�ɍ������ށB�I�V���X�R�[�v�̃W���b�N�ƃ^�[�~�i���̐F�������ɂȂ�悤�ɂ���B
(12) �d���X�C�b�`�r�P���I���ɂ���B
(13) ����������\�������邽�߂ɁADC-AC��ւ��X�C�b�`��DC�ɐ�ւ���B
(14) ���̎��̔g�`���O���t�p���ɏ������B
(15) �d���X�C�b�`�r�P���I�t�ɂ���B
(16) �s�R�Ƃs�S�ɍ������I�V���X�R�[�v�̃W���b�N���������O���A�s�T�Ƃs�U�ɍ������ށB�I�V���X�R�[�v�̃W���b�N�ƃ^�[�~�i���̐F�������ɂȂ�悤�ɂ���B
(17) ������H�̃R���f���T�[�̃X�C�b�`�r�Q�Ƃr�R���I�t�ɂ���B
(18) �d���X�C�b�`�r�P���I���ɂ���B
(19) ���̎��̔g�`���O���t�p���ɏ������B
(20) ������H�̓���m�F������B�r�Q���I���ɂ���B���̏�Ԃʼn�H��100�ʂe�̃R���f���T�[���ڑ����ꂽ���ƂɂȂ�B
(21) ���̎��̔g�`���O���t�p���ɏ������B
(22) �R���f���T�[�̗e�ʂ�傫������B�R���f���T�[�̃X�C�b�`�r�Q���I�t�ɂ��āA�r�R���I���ɂ���B���̏�Ԃʼn�H��2200�ʂe�̃R���f���T�[���ڑ����ꂽ���ƂɂȂ�B
(23) ���̎��̔g�`���O���t�p���ɏ������B
(24) ���ׂĂ̎������I�������̂ŁA�I�V���X�R�[�v�̓d�����I�t�ɂ��A����ɓd���X�C�b�`�r�P���I�t�ɂ���B�R���Z���g����v���O���B
�@�i�U�j���ʂƍl�@
(1) �����Ŋώ@���ꂽ�g�����X�̓��g�`�A���g������H�̒����g�`�A�S�g������H�̒����g�`�A������H�̒����g�`(�Q�̗e�ʂ��قȂ�R���f���T�[)�̌v�T�̔g�`���O���t�ɂ܂Ƃ߂��B�����̃O���t�͍Ō�̃y�[�W�Ɏ����B�܂��A�e�f�q�Ɣg�`�Ƃ̊W�͈ȉ��̒ʂ�ł���B
�@�@�@�@���g�����X�@�@�@�@�d����ψ�����(�~������)�B�g�`�̐U�蕝���������Ȃ�B
�@�@�@�@���_�C�I�[�h�@�@�@�d����������ւƂȂ����A���̋t�����ւ͓d���𗬂��Ȃ��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�g�`�́A�}�C�i�X�����܂��̓v���X�����̂݊ώ@�����B
�@�@�@�@���R���f���T�[�@�@�d�C�̓��̂ɑ��ʂ̓d�ׂ�~�ςł��鑕�u�B�g�`�̓R���f���T�[�ɗ��܂����d�ׂŁA�𗬗v�f(���̓d��)�����Ȃ��Ȃ�B
���u���b�W�_�C�I�[�h�@�@�S�̃_�C�I�[�h�ɂ���ău���b�W���g�܂ꂽ������H�B���ג�R�����̓d���̗��������͐������̓����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�g�`�͕��̗̈�����Ԏ��Ő܂�Ԃ����`�ɂȂ�
�@�@�@(2)�}�Q(��)�̉�H�œd���̗�����𗬔g�`�̂P�T�C�N���ɂ��ď����B
���ӂ��ׂ��_���ӏ������ɂ���B
�@�@�_�C�I�[�h�́��ׂ��Ȃ���ɂ����d���͗���Ȃ��B
�@�A�d���͓d�ʂ̍������ɂ͗���邱�Ƃ͏o���Ȃ��B
�@�B�𗬔g�`�P�T�C�N���ł́A�d���̗�������(�d��)�͐��ƕ��̂Q����B
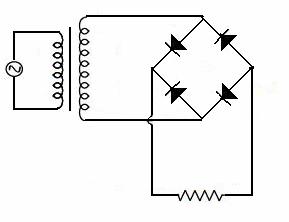
�}�Q�@�d�������̏ꍇ

�}�R�@�d�������̏ꍇ
�T�D�X�C�b�`���O��H
�@(�T)��������
�@�@�@�ϒ�R�q�Q��ς��邱�Ƃŏo�͓d����0.5[�u]���݂ŕς��Ȃ���A���̎���cycle���Ԃɑ���on���Ԃ̒l��}�V�̂悤�ɂ܂Ƃ߂�B
�@�@�@���j�q�Q�̓e�L�X�g�P�Q�y�[�W�̐}�U���̒�R�ł���B�܂��A�}�V�̓e�L�X�g�P�R�y�[�W�̂��̂ł���B
�@�i�U�j����
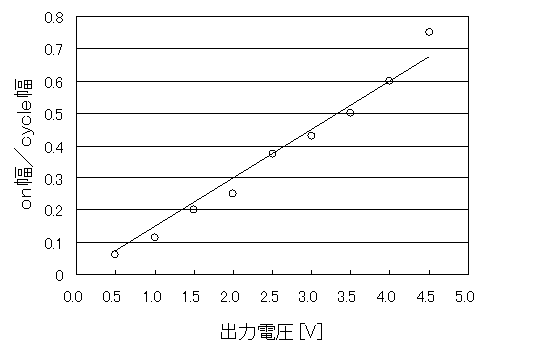
�@�@�@�@�@���肳�ꂽ���ʂ��ȉ��̕\�T�Ɏ����B�܂��A�d����on���^cycle���̊W���������O���t�͎��̃y�[�W�̐}�S�Ɏ����B
�\�T�@on����off���Ƃ��̊W�l
|
�d�� [�u] |
on�� [mm] |
off�� [mm] |
cycle�� [mm] |
on���^cycle�� |
|
0.5 |
3 |
45 |
48 |
0.063 |
|
1.0 |
3 |
23 |
26 |
0.115 |
|
1.5 |
3 |
12 |
15 |
0.200 |
|
2.0 |
3 |
9 |
12 |
0.250 |
|
2.5 |
3 |
5 |
8 |
0.375 |
|
3.0 |
3 |
4 |
7 |
0.429 |
|
3.5 |
3 |
3 |
6 |
0.500 |
|
4.0 |
3 |
2 |
5 |
0.600 |
|
4.5 |
3 |
1 |
4 |
0.750 |
�U�D�Q�l����
�@�@�����B���F����@�d�C�d�q�H�w�̊�b�����A�I�[���ЁA1981
�����H�Ƒ�w�H�w�������H�ƍ��Z�@�Ȋw�Z�p������ҁF�Ȋw�Z�p��b�i���j�A2000