1.目的
一定の温度および圧力の元で、トルエンと水が2層をなして混ざらない。そこに安息香酸を加えると、安息香酸が2層に溶解し平衡に達する。このことを踏まえ、実験を通して分配の法則と分子の会合を理解する。
2.実験原理
まったく溶け合わない2種類の液体AとBに、両者に溶ける別の物質Xを溶かした場合、XのA層とB層での濃度をそれぞれCA,CBとすると、一般的に次式が成り立つ。ただし、物質Xが分配平衡に達したときである。
![]() (1)
(1)
ここで、A層で物質Xが1分子でまま存在し、B層ではn分子が会合しているとすると、(1)より次式が導ける。
![]() (2)
(2)
各層の物質Xの化学ポテンシャルをとり、2層で分配平衡に達していることに注意して式(2)に代入すれば、KDが温度のみに依存し、一定温度では一定の値をとることがわかる。
また、式(2)の両辺の対数をとると、
nlog CA - logCB = log KD (3)
になる。このことにより、直線関係を示せばB相中の物質Xの会合数nを求めることが出来る。
しかし、安息香酸はカルボン酸であるので、下記の図1で示すように2分子が会合していることが容易に想定できる。実際に実験により算出される会合数がどれだけ、理論値からずれているかもわかる。
図1 安息香酸の会合
3.実験方法
実験開始前に、恒温槽の電源を入れ温度を25℃に設定する。
[1日目]
(i)約10M水酸化ナトリウム溶液を5ml量りとり、500mlのポリビンに移してイオン交換水で約0.1Mに希釈する。ファクター(f=1.080)の0.1M フタル酸水素カリウム(KHP)溶液で約0.1Mに調製した水酸化ナトリウム溶液の濃度を標定する。被滴下のフタル酸水素カリウム溶液はホールピペットを用い、20mlをコニカルビーカーに入れ滴定する。これを2回以上行い、平均値を用いて水酸化ナトリウム濃度を決定する。
(ii)電子天秤を用いて、安息香酸を0.5gおよび1.0g(2日目は1.5gと2.0gである)をそれぞれ量りとり、200ml三角フラスコに入れる。メスシリンダーでトルエンを60ml量りとり、それぞれの三角フラスコに移し、安息香酸を完全に溶解させる。溶解させた後、それぞれの三角フラスコから20mlホールピペットを用いて20mlを採取し、ケルダールフラスコに入れる。最初に秤量した安息香酸の量が少ない物から順位に、No.1~No.4と番号を付ける。
(iii)各ケルダールフラスコにホープピペットを用いて精製水50mlを加え、コルク栓をして高温槽に浸す。
(iv)5分ごとに各フラスコを恒温層から取り出し、よく攪拌し2層を混ぜ合わせる。この操作を7回繰り返す。7回攪拌を繰り返したことで、分配平衡に達したこととする。
(v)最後に攪拌してから約5分、液層が2層に分かれたら、水層(下層)を20mlホールピペットで採取し、(i)で標定したNaOHaqで滴定する。これを各試料No.1~No.4について行う。ただし、1日目はNo.1とNo.2に行う。
(vi)トルエン層(油層―上層)は直接NaOHaqで滴定することは事実上不可能なため、逆滴定を行い、トルエン層の安息香酸の濃度を求める。No.1の試料では0.1M NaOHaq 25mlを分液ロートに入れ、さらにケルダールフラスコのトルエン層を20ml分取して、これも分液ロートに入れよく攪拌する。フェノールフタレイン指示薬を数滴加えて再びよく攪拌し、水層(下層)がアルカリ性(赤紫色)であることを確認して、水層をコニカルビーカーに取り出す。ただし、分液ロートに入れる0.1M NaOHaqの量はNo.2,No.3, No.4,それぞれ40ml,55ml,70mlである、
(vii)分液ロートにさらに精製水を5ml加えて、よく攪拌しトルエン層を洗浄する。水層を(vi)で水層を取ったコニカルビーカーに入れ、フタル酸水素カリウムで滴定をする。
[2日目]
2日目は安息香酸の量を1.5gと2.0gにして実験を行う。その他、異なるとことは上記にも示してあるが、分液ロートに入れる0.1M NaOHaqの量が55mlと70mlになることのみである。
4.結果とまとめ
(1) 各日に得られたデータから水酸化ナトリウムと安息香酸の濃度を求める。
[1日目]
(i)0.1[mol/L] NaOHaqの標定
0.1[mol/L] KHPaqのfactor f=1.080
0.1[mol/L] NaOHaqの滴定量
1回目 20.16 [ml]
2回目 20.17 [ml]
0.1[mol/L] NaOHaqの濃度をCとすると
0.1 ×1.080 ×20 =C × (20.16+20.17) /2
∴ C =0.107116
=0.1071 [mol/L]
0.1[mol/L] NaOHaqのfactor
f=0.1071 /0.1000 =1.071
(ii)水層中の安息香酸の濃度CW
滴定回数は溶液の量の関係上、1回しか行わなかった。
|
NaOHaqの量 |
No.1 |
No.2 |
|
滴定前 |
0.00 |
0.00 |
|
滴定後 |
1.55 |
2.11 |
|
NaOHaqの滴下量 |
1.55 |
2.11 |
No.1 ; 0.1071 ×1.55 =CW ×20
∴ CW =0.00830025
=0.00830
=8.30×10-3 [mol/L]
No.2 ; 0.1071 ×2.11 =CW ×20
∴ CW =0.0112990
=0.0113
=1.13×10-2 [mol/L]
(iii)トルエン層中の安息香酸の濃度CT
逆滴定を行い、トルエン層中の安息香酸の濃度CTを求める。だだし、逆滴定をする際に先に入れた0.1[mol/L] NaOHaqの量は、No.1が25ml、No.2が40mlである。
|
KHPaqの量 |
No.1
① |
② |
No.2 |
|
滴定前 |
0.00 |
0.00 |
0.00 |
|
滴定後 |
16.48 |
12.83 |
14.45 |
|
KHPaqの滴下量[ml] |
16.48 |
12.83 |
14.45 |
No.1の1回目のKHPaqの滴定量が、No.2のKHPaqの滴定量より多いので、再 びNo.1の滴定を行った。その値がNo.1 ②である。明らかにNo.1の1回目のKHPaqの滴定量はおかしいので、安息香酸の濃度CTを算出する時にはNo.1 ②の値を用いる。
No.1 ; 0.1071 ×25=CT ×20 +0.1 ×1.080 ×12.83
∴ CT =0.064593
=0.06459
=6.459×10-2 [mol/L]
No.2 ; 0.1071 ×40=CT ×20 +0.1 ×1.080 ×12.83
∴ CT=0.13617
=0.1362
=1.365×10-1 [mol/L]
[2日目]
(i)水層中の安息香酸の濃度CW
滴定回数は溶液の量の関係上、1回しか行わなかった。
|
NaOHaqの量 |
No.3 |
No.4 |
|
滴定前 |
0.00 |
0.00 |
|
滴定後 |
2.87 |
3.22 |
|
NaOHaqの滴下量[ml] |
2.87 |
3.22 |
No.1 ; 0.1071 ×2.87 =CW ×20
∴ CW =0.0153688
=0.0154
=1.54×10-2 [mol/L]
No.2 ; 0.1071 ×3.22 =CW ×20
∴ CW =0.0172431
=0.0172
=1.72×10-2 [mol/L]
(ii)トルエン層中の安息香酸の濃度CT
逆滴定を行い、トルエン層中の安息香酸の濃度CTを求める。だだし、逆滴定をする際に先に入れた0.1[mol/L] NaOHaqの量は、No.3が55ml、No.4が70mlである。
|
NaOHaqの量 |
No.3 |
No.4 |
|
滴定前 |
0.00 |
0.00 |
|
滴定後 |
17.59 |
19.47 |
|
NaOHaqの滴下量[ml] |
17.59 |
19.47 |
No.3 ; 0.1071 ×55=CT ×20 +0.1 ×1.080 ×17.59
∴ CT =0.199539
=0.1995
=1.995×10-1 [mol/L]
No.4 ; 0.1071 ×70=CT ×20 +0.1 ×1.080 ×19.47
∴ CT=0.269712
=0.2697
=2.697×10-1 [mol/L]
(2) 上記の結果を基にして、分配の法則の式(3)に必要な因子についての計算を行い、
求めた値を表にまとめた。
表1 各層の安息香酸の濃度とその対数
|
|
No.1 |
No.2 |
No.3 |
No.4 |
|
CW [mol/L] |
8.30×10-3 |
1.13×10-2 |
1.54×10-2 |
1.72×10-2 |
|
CT [mol/L] |
6.459×10-2 |
1.365×10-1 |
1.995×10-1 |
2.697×10-1 |
|
log CW |
-2.081 |
-1.947 |
-1.813 |
-1.778 |
|
log CT |
-1.190 |
-0.8659 |
-0.7001 |
-0.5691 |
注)本来、log CWの有効数字は3であるが、上記の2つの表のlog CTの有効数字が4桁になるのでlog CWも有効数字を4桁にしてある。その理由は有効数字を4桁にすることでグラフを作成する際に、上記の2つの表のlog CWを用いるためより、グラフから切片log KD、 傾きnを求める際にある程度の誤差が出来てしまうと考えたためである。
(3)表1の値を基にして、実験原理で示した式(3)に代入してグラフを作成した。
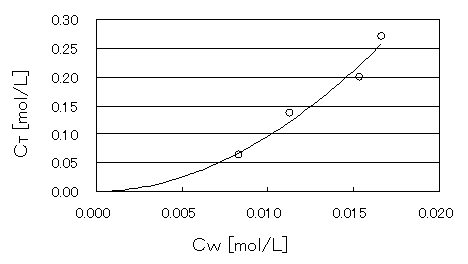
図1 会合数と分配率の関係
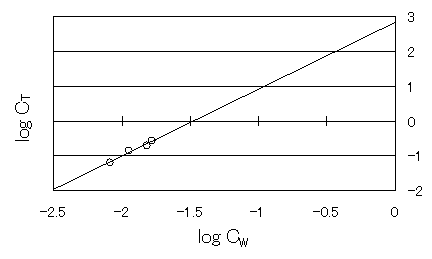
図2 CTとCWの対数をとった関係
図2を描いた事により、直線の式を求めることが出来る。そのことにより、切片からlog KD、 傾きからnを求めることが出来る。
log CT = 1.9213 log CW + 2.8287
=1.9213 log CW -log 10-2.8287
=1.9213 log CW -log (1.48354×10-3)
=1.921 log CW -log (1.484×10-3)
よって、会合数nおよび分配率 KDは、
n=1.921 KD =1.484×10-3
である。
また、平均二乗誤差R2は、R2=0.9772であった。会合数nと分配率KDが求まったので、図1の関係式を求めることが出来る。
CT =1/KD ×CWn
=1/(1.484×10-3)×CW1.921
=673.9CW1.921
(4)この実験で得た値を各種の比をとった。ここでは、n=1.921である。
表2 各濃度の比とその関係
|
|
No.1 |
No.2 |
No.3 |
No.4 |
|
CW |
0.00830 |
0.01130 |
0.01537 |
0.01665 |
|
CT |
0.06459 |
0.1361 |
0.1995 |
0.2697 |
|
CW/CT |
0.1285 |
0.0829 |
0.07703 |
0.06175 |
|
CT/CW |
7.782 |
12.05 |
12.98 |
16.19 |
|
CWn/CT |
0.001555 |
0.001334 |
0.001644 |
0.001419 |
|
CW2/CT |
0.001067 |
0.0009376 |
0.001184 |
0.001028 |
実際の系では溶質が今回のように会合をしていたり、解離,錯体生成などを起こすことが多い。分析や分離をする場合、溶質の化学種に関係なく、両相における溶質の全分析濃度の比はわかりやすく重要である。分配比Dは![]() で定義される。
で定義される。
今回の実験での分配率DはCT/CWである。
安息香酸の参考値を上げる。(化学便覧より引用)
表3 分配比
|
溶媒α |
溶媒β |
θ/℃ |
[A]α/mol dm-3 |
分配比D |
|
ベンゼン |
水 |
25 |
0.0015 |
1.75 ± 0.02 |
|
|
|
|
0.2 |
15.6 ± 0.5 |
(5)恒温層中の温度
実験前の温度は、恒温層が温まっているのを確認し測定した。
|
|
実験前 |
実験後 |
誤差 |
|
1日目 |
25.0℃ |
25.0℃ |
± 0.0℃ |
|
2日目 |
24.8℃ |
25.1℃ |
± 0.3℃ |
5.考察
0.1M NaOHaqの標定ために行った滴定では、終点の目安であるフェノールフタレイン変色が各回でうすい赤紫色になった。さらに、滴定量の誤差も100分の1であるとことから、NaOHの濃度の誤差は非常に小さいと考えられる。
また今回の実験の滴定は0.1M NaOHaqの標定を除いて、各濃度を決定するために行った滴定は溶液の関係上1回しか原則的に行わなかった。そのことを考えると、実験結果は大変大雑把な値になっている可能性もある。
No.1のCTを求める際に行った滴定で、1回目の滴定量がNo.2の滴定量よりも多くなってしまった原因を考える。ビュレット内のKHPaqをすべて捨てて、KHPaqで共洗いした後に、2回目の滴定を行った値が他の班の値に近いことから以下のことが原因ではないかと思う。KHPaqが入っていたビュレットに誤って、精製水またはNaOHaqを入れてしまったことである。
見づらいかもしれないが図2を見れば、測定値から算出したlog CTとlog CTの値が直線の関係であるのは明白である。また、その近似直線の平均二乗誤差R2はR2=0.9772であった。この値が1.000に比較的近いことからもlog CTとlog CWが比例関係であると言える。
表2から、安息香酸は水層よりも油層に溶けやすいことがわかる。また、CTは物質量に比例して増加しているが、CWの傾向はあまり良くわからない。安息香酸は冷水に難溶なため溶解度が低く、物質量の増加に応じて濃度上昇が見られなかったのだと思う。分配比DであるCT/CWは溶質の量に従い増加している。このことから、CTの方がCWより濃度の上昇率よりも大きいことがわかる。分配比Dを表3のベンゼンの値と比較する。最も近い条件はNo.3で、分配比DはD=12.98である。ベンゼンの分配比DがD=15.6 ± 0.5であることを考えると、安息香酸はトルエンよりもベンゼンに溶けやすいのだと思う。その理由として考えられるのは、トルエンはベンゼンに水素がメチル基に置換された物質であるのでベンゼンよりも分子内に極性があるために、安息香酸の溶解量が少なくなったためではないかと思う。
また、CWn/CT (n=1.921)がほぼ一定範囲も値になっていることから分配の法則が成り立っているのではないかと思う。会合数nの理論値はn=2である。同様にCWn/CTを求めると、誤差範囲がn=1.921では3.1×10-4であったが、2.4×10-4となり、誤差範囲が小さくなったので、実際の会合数nは極めて2に近いのではないかと思う。
図1と図2を見てもわかるように、各日の実験を行った順番で同様の傾向が出ている。分析する方法は多数あるが、その日の2回目に求めたCTが1回目に求めたものより近似線から上に外れているのがわかる。滴定などでの誤差は一般的に考えてほぼ等しいと考えられる。よって、その他の操作時に原因があると考えられる。考えられる原因は、水層とトルエン層の2層を一緒にしていた時間に差が出てしまったことである。必然的に後時に実験する方が前の滴定で手間取ってしまった時間分、2層を一緒にしてしまっていた状況が生じた。その時間分、より分配平衡状態に近い状況になったのではないかと、考えられる。
6.感想
分配比を使っての計算は今までに行ったことがあったが、分配の法則を用いて会合度などを求められることを初めて知った。
また、前回の実験で滴定のテクニックが身に付いたので実験自体もスムーズに進めることができた。今回行った実験も、これから役に立つ内容であったので以後の実験にいかして生きたい。
7.参考文献
化学実験テキスト研究会編:図解・化学実験シリーズ1 基礎化学実験、産業図書
P.W.アトキンス著:第六版 物理化学(下)、東京化学同人
津田栄著:改訂新版 化学通論、朝倉書店
玉虫文一ら著:第3版増補版 理化学事典、岩波書店
日本化学会編:改訂5編 化学便覧 基礎化学編 Ⅱ、丸善